Code: https://github.com/nrsyed/proboards-scraper
Documentation: https://nrsyed.github.io/proboards-scraper
- Part 1: Introduction and background
- Part 2: Implementation (project structure and scraper initialization)
- Part 3: Implementation (scraper internals)
This post follows from Part 2 and continues delving into the code, examining the manner in which users and threads are scraped. We’ll follow the flow of data through the program, seeing how the various functions and classes interact.
Scraping a user
In the last post, we saw that scraping user profiles starts with defining an async task for scraping user profiles in run_scraper() (located in the file core.py), adding that task to the list of async tasks to complete, and running those tasks in the asyncio event loop. The relevant lines are shown together below:
users_task = _task_wrapper(scrape_users, "both", url, manager)
...
if users_task is not None:
tasks.append(users_task)
else:
manager.user_queue = None
if content_task is not None:
tasks.append(content_task)
database_task = manager.run()
tasks.append(database_task)
task_group = asyncio.gather(*tasks)
asyncio.get_event_loop().run_until_complete(task_group)This tells the event loop to asynchronously run scrape_users(), which is defined in scrape.py, a task for scraping content if selected (e.g., scrape_forum()), and ScraperManager.run(). This is the definition for scrape_users():
|
|
On line 239, we get the page source (note that ScraperManager.get_source() is awaitable, which means that, at this point, the event loop can suspend execution of this task and switch to a different task). We’ll examine ScraperManager.get_source() later—for now, just know that it’s a wrapper around asyncio.ClientSession.get() and fetches the HTML page source of a URL. The next few lines grab links to all the user profiles from the list of members on the current page and on all subsequent pages. Lines 252-259 create an async task for each user profile (by calling scrape_user() on the profile URL) and add them to the event loop, then wait for them to finish.
Here are the first few lines of scrape_user():
|
|
This initializes the dictionary that will later be used to construct a SQLAlchemy User object. The items in this dictionary will serve as keyword arguments to the User constructor.
We won’t go through the entire function, as there’s a considerable amount of
code that parses the HTML via BeautifulSoup, but the following snippet provides
a glimpse of what some of that code looks like. Observe how the extracted
information is added to the user dictionary.
|
|
Near the end of the function, we put user in the queue:
|
|
Let’s jump to ScraperManager.run(), which lives in scraper_manager.py, and see how it handles items in the user queue.
|
|
Above, we see that it pops items (dictionaries like user) from the queue
and calls Database.insert_user() to insert them into the database.
Let’s jump to database.py to see how Database.insert_user() is defined:
|
|
Database.insert_user() wraps a more generic method, Database.insert(), which accepts a table metaclass instance of any type (e.g., Board, Thread, User). The definition for Database.insert() is shown below with its lengthy docstring removed for brevity.
def insert(
self,
obj: sqlalchemy.orm.DeclarativeMeta,
filters: dict = None,
update: bool = False
) -> Tuple[int, sqlalchemy.orm.DeclarativeMeta]:
if filters is None:
filters = {"id": obj.id}
Metaclass = type(obj)
result = self.session.query(Metaclass).filter_by(**filters).first()
inserted = 0
if result is None:
self.session.add(obj)
self.session.commit()
inserted = 1
ret = obj
elif result is not None and update:
for attr, val in vars(obj).items():
if not attr.startswith("_"):
setattr(result, attr, val)
self.session.commit()
inserted = 2
ret = result
else:
ret = result
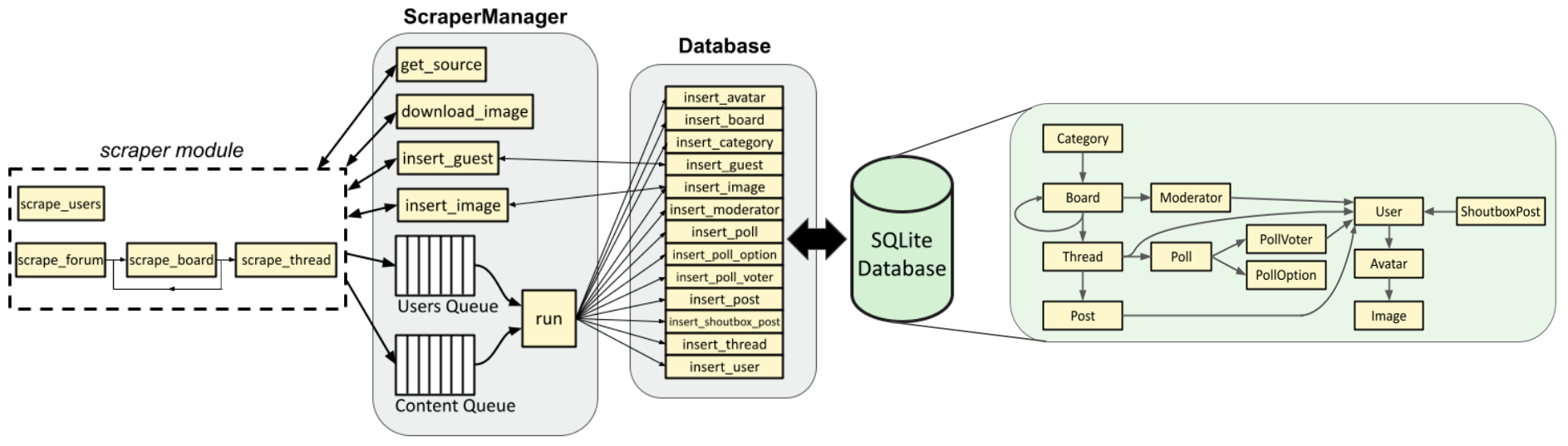
return inserted, retThe method returns an “insert code” and the SQLAlchemy table object—i.e., a User instance. In this case, ScraperManager.run(), which called Database.insert_user(), doesn’t use the return value, but in other cases, the value returned by the insert method will be used. Recall the scraper architecture diagram, whose arrows illustrate this:
In fact, ScraperManager.run() doesn’t care about the return values at all, hence the single-ended arrows that point from run() to the insert methods. ScraperManager.insert_guest() and ScraperManager.insert_image(), on the other hand, do need to capture those values. We’ll see this in the next section.
Downloading and adding images
Unlike other objects, images are actually downloaded to disk, and an Image that references said file is inserted into the database. Continuing through scrape_user(): that function eventually grabs the URL for the user’s avatar (profile picture) and makes an attempt to download that avatar.
|
|
Again, this is awaitable—the event loop can switch to another task while it waits for ScraperManager.download_image() to finish. Here is its definition:
|
|
It’s actually a wrapper around a helper function of the same name. Don’t
worry about the if-statement and self._delay() for now—we’ll get to
that later. The download_image() helper function is located at the top
level of the package and is defined in http_requests.py. It returns a
dictionary containing information on the download HTTP request and, if
successful, bytes representing the downloaded file itself. The function
first initializes this dictionary with None values:
|
|
Note that an Image (and Avatar) is added to the database regardless of whether the file is successfully downloaded; the database entry serves as a record of the forum’s reference to the image even if we don’t have the image on disk. This usually occurs if the image’s URL no longer exists, which is likely since some forums are decades old and contain numerous dead links to sites that have long since disappeared from the web.
The rest of the function makes an awaitable HTTP request, handles the response, does some error checking, writes the downloaded image to disk if it’s a valid image and the file doesn’t already exist, and updates/returns the dictionary.
|
|
When we write the file to disk, we use the MD5 hash of the image file to generate a unique filename and avoid collisions in case several images have the same (original) filename.
Let’s jump back to scrape_user() to see how the dictionary returned by ScraperManager.download_image() (and download_image()) is used to insert the image entry into the database:
|
|
Scraping a thread
Scraping content (like a thread) is largely similar to that of scraping users, but differs in a couple ways. Let’s use scrape_thread() (found in scrape.py) to explore these differences.
The function first grabs the page source as before, extracts some basic information about the thread (the thread ID, the thread title, whether the thread is locked or stickied, etc.). Before scraping the posts, we first check whether the create user is a guest:
|
|
Like adding an image, adding a guest deviates from the async queue workflow. Instead, ScraperManager.insert_guest() is called:
|
|
In this case, we construct a dictionary similar to that for a User, since a guest is a special case of user, but there’s no information on the guest besides their name. We then call Database.insert_guest(), which looks like this (docstring removed):
def insert_guest(self, guest_: dict) -> User:
guest = User(**guest_)
# Query the database for all existing guests (negative user id).
query = self.session.query(User).filter(User.id < 0)
# Of the existing guests, query for the name of the current guest.
this_guest = query.filter_by(name=guest.name).first()
if this_guest:
# This guest user already exists in the database.
guest.id = this_guest.id
else:
# Otherwise, this particular guest user does not exist in the
# database. Iterate through all guests and assign a new negative
# user id by decrementing the smallest guest user id already in
# the database.
lowest_id = 0
for existing_guest in query.all():
lowest_id = min(existing_guest.id, lowest_id)
new_guest_id = lowest_id - 1
guest.id = new_guest_id
inserted, guest = self.insert(guest)
self._insert_log_msg(f"Guest {guest.name}", inserted)
return guestHere, we query for all users in the database with a negative ID. Of the results (if any), we look for one whose name matches the guest we’ve encountered. If there’s a result, we set the encountered guest’s user ID to that from the result. If there isn’t a result, we find the smallest existing ID among the guests in the database and decrement it to generate a negative user ID for the new guest. After being inserted into the database, the User instance corresponding to the guest is returned to ScraperManager.insert_guest(), which then returns the user ID to scrape_thread().
Jumping back to scrape_thread(), the next order of business is to scrape the poll associated with the thread, if there is one. The way ProBoards forums work, poll modal windows are inserted into the page HTML source by JavaScript. This means we need to use Selenium to load the page source if a poll is present instead of relying on the source obtained from the aiohttp session.
|
|
Why do we use time.sleep(), which blocks the thread, instead of
await asyncio.sleep(), which would allow the event loop to schedule other
tasks? A Selenium WebDriver session is basically a single browser window.
Because we’re just passing around and using the same Selenium session (via
the ScraperManager’s driver attribute), if multiple polls are being scraped
concurrently, the WebDriver instance can load only one page at a time, and
all the currently active scrape_poll() tasks would end up parsing the source
for the same poll. Since the WebDriver is a Chrome browser, we could open a
new tab for each poll, but keeping track of them and switching between them
adds a layer of unnecessary complexity and a potential source of bugs. We
could also create a new WebDriver instance for each poll, but that introduces
overhead. Either way, this would likely not be a bottleneck and I figured the
easiest solution was to wait for each WebDriver request.
We won’t delve into the scrape_poll() function. It parses the HTML from the Selenium WebDriver using BeautifulSoup like we’ve already seen.
In the middle of scrape_thread(), we add the thread to the content queue:
|
|
This is similar to adding a user to the user queue except there’s a "type"
key that tells ScraperManager.run() which Database method to call. Here is the
relevant logic in ScraperManager.run():
|
|
Note that the "type" key is deleted before passing the dictionary to the
insert function because the dictionary serves as a source of keyword arguments
for the table metaclass constructor (which doesn’t expect to receive that
keyword). In other words, the Thread constructor doesn’t take a type
argument.
The rest of scrape_thread() iterates over the pages of the thread and grabs all the posts on each page. This is achieved with a while loop in which it finds the “next page” button on the page and determines whether the button is disabled (which occurs on the last page of a thread).
|
|
Rate limiting
Hitting a server with a lot of HTTP requests can result in future requests being throttled or blocked altogether. To address this, we incorporate request rate-limiting via the ScraperManager. Consider the ScraperManager.get_source() method:
|
|
The method calls a private helper method named ScraperManager._delay(), defined as follows:
|
|
This causes the calling task to wait for a “short” amount of time (1.5 seconds
by default) before making an HTTP request, except every request_threshold
requests (15 by default) when the wait is longer (20 seconds by default).
There’s nothing special about these numbers and they can be adjusted
for a given application. Note that, because this utilizes asyncio.sleep(),
other tasks can continue to make HTTP requests (subject to the same short/long
sleep constraints). A more aggressive alternative would be to use time.sleep(),
which would block the thread and force all tasks to wait.
Conclusion
In our journey through the internals of the scraper, we’ve tackled asyncio, HTTP requests/sessions, and SQLAlchemy database management. I don’t claim to be an expert on web scraping, but I like to think this implementation for this particular scenario was logically crafted and sufficiently modular to generalize to other web scraping challenges. Happy coding, and please scrape responsibly!
