Link to code: https://github.com/nrsyed/pytorch-yolov3
- Part 1 (Background)
- Part 2 (Initializing the network)
- Part 3 (Inference)
- Part 4 (Real-time multithreaded detection)
- Part 5 (Command-line interface)
YOLOv3, the third iteration of Joseph Redmon et al’s YOLO (“You Only Look Once”) Darknet-based object detection neural network architecture, was developed and published in 2018 (link to paper). The defining characteristic of YOLO is that it combines object detection (“is there an object?”), classification (“what kind of object is it?”), and localization (“where in the image is the object?”) in a single pass through the network. This makes it more computationally efficient and robust than other networks that only perform one or two of these tasks simultaneously.
The original Darknet/YOLO code is written in C, making it performant but more difficult to understand and play around with than if it were written in Python (my personal favorite language) using a framework like PyTorch (my personal favorite deep learning framework). Before taking a deep dive into the background and my implementation, let’s look at an example of the end result for real-time object detection on a webcam video stream:
This post will touch on the background and fundamental theory behind YOLOv3, while the next post will examine the code and implementation.
How does YOLOv3 work?
Let’s use the following sample image taken from the COCO 2017 validation dataset:

The classification layer of the YOLO network divides this image into a grid of cells. For illustration, let’s say it’s a 7×7 grid, which would look like the following (in the actual algorithm, there are three distinct grid sizes corresponding to different scales at different layers of the network—we’ll get to that in a minute):

YOLO makes use of bounding box “priors” or “anchors”. These are predefined bounding boxes whose shape and size is similar to those of objects in the training dataset. The authors of YOLO used K-means clustering to cluster the bounding boxes of objects in the training data to determine suitable anchor box sizes. These anchor boxes essentially serve as a guideline for the algorithm to look for objects of similar size and shape. The YOLO classification layer uses three anchor boxes; thus, at each grid cell in the image above, it makes a prediction for each of three bounding boxes based on the three anchor boxes.
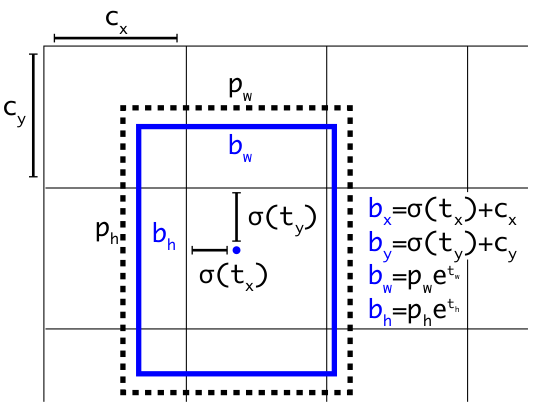
In the figure above, which is taken from the YOLOv3 paper, the dashed box represents an anchor box whose width and height are given by pw and ph, respectively. The network predicts parameters tw and th that, when exponentiated, scale the anchor box dimensions to fit the detected object. The network also predicts the x/y position of the center of the bounding box within the cell via the parameters tx and ty, respectively (note that the sigmoid function must be applied to the raw values first). The x/y center of the bounding box with respect to the image origin is obtained by adding the offset of the cell origin from the image origin, given by cx and cy, to the offset of the bounding box center from the cell origin. This yields the final predicted bounding box, shown in blue.
For a 7×7 grid, there would be 49 cells each predicting three bounding boxes for a total of 147 bounding boxes. That’s a lot of predictions! However, for each bounding box, the algorithm also predicts an “objectness” score—the likelihood that the predicted bounding box actually contains an object—as well as a class score for each class, which represent the likelihood of the object belonging to each class. This allows us to filter out detections with low probabilities.
Network architecture and design
While there are several variations of YOLOv3, they all share the Darknet-53 backbone, which comprises the first 74 layers and is so named because it contains 53 convolutional layers. The lengthy table below details the layer types and layer input/output shapes for a 608×608 input image. There are a couple special layer types, namely “shortcut” (which is a residual layer that sums the outputs of several previous layers) and “route” (which concatenates the outputs of one or more previous layers). For the shortcut and route layers, the table specifies layer indices. For example, layer 4 is a shortcut layer whose Input column contains “[3, 1]”, which indicates that the output feature maps from layers 3 and 1 are summed. The result becomes the input for layer 5. Some route layers only contain a single layer index, like layer 83 whose input is “[79]”—in other words, this is a skip connection that simply takes the output from layer 79 and makes it the input for layer 80. On the other hand, layer 86 is a route layer with inputs “[85, 61]”—in other words, it concatenates the feature maps from layers 85 and 61. Finally, there are three YOLO classification layers; each one makes predictions at a different scale.
| Layer # | Type | Input | Output shape |
|---|---|---|---|
| convolutional | (3, 608, 608) | (32, 608, 608) | |
| 1 | convolutional | (32, 608, 608) | (64, 304, 304) |
| 2 | convolutional | (64, 304, 304) | (32, 304, 304) |
| 3 | convolutional | (32, 304, 304) | (64, 304, 304) |
| 4 | shortcut | [3, 1] | (64, 304, 304) |
| 5 | convolutional | (64, 304, 304) | (128, 152, 152) |
| 6 | convolutional | (128, 152, 152) | (64, 152, 152) |
| 7 | convolutional | (64, 152, 152) | (128, 152, 152) |
| 8 | shortcut | [7, 5] | (128, 152, 152) |
| 9 | convolutional | (128, 152, 152) | (64, 152, 152) |
| 10 | convolutional | (64, 152, 152) | (128, 152, 152) |
| 11 | shortcut | [10, 8] | (128, 152, 152) |
| 12 | convolutional | (128, 152, 152) | (256, 76, 76) |
| 13 | convolutional | (256, 76, 76) | (128, 76, 76) |
| 14 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 15 | shortcut | [14, 12] | (256, 76, 76) |
| 16 | convolutional | (256, 76, 76) | (128, 76, 76) |
| 17 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 18 | shortcut | [17, 15] | (256, 76, 76) |
| 19 | convolutional | (256, 76, 76) | (128, 76, 76) |
| 20 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 21 | shortcut | [20, 18] | (256, 76, 76) |
| 22 | convolutional | (256, 76, 76) | (128, 76, 76) |
| 23 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 24 | shortcut | [23, 21] | (256, 76, 76) |
| 25 | convolutional | (256, 76, 76) | (128, 76, 76) |
| 26 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 27 | shortcut | [26, 24] | (256, 76, 76) |
| 28 | convolutional | (256, 76, 76) | (128, 76, 76) |
| 29 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 30 | shortcut | [29, 27] | (256, 76, 76) |
| 31 | convolutional | (256, 76, 76) | (128, 76, 76) |
| 32 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 33 | shortcut | [32, 30] | (256, 76, 76) |
| 34 | convolutional | (256, 76, 76) | (128, 76, 76) |
| 35 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 36 | shortcut | [35, 33] | (256, 76, 76) |
| 37 | convolutional | (256, 76, 76) | (512, 38, 38) |
| 38 | convolutional | (512, 38, 38) | (256, 38, 38) |
| 39 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 40 | shortcut | [39, 37] | (512, 38, 38) |
| 41 | convolutional | (512, 38, 38) | (256, 38, 38) |
| 42 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 43 | shortcut | [42, 40] | (512, 38, 38) |
| 44 | convolutional | (512, 38, 38) | (256, 38, 38) |
| 45 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 46 | shortcut | [45, 43] | (512, 38, 38) |
| 47 | convolutional | (512, 38, 38) | (256, 38, 38) |
| 48 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 49 | shortcut | [48, 46] | (512, 38, 38) |
| 50 | convolutional | (512, 38, 38) | (256, 38, 38) |
| 51 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 52 | shortcut | [51, 49] | (512, 38, 38) |
| 53 | convolutional | (512, 38, 38) | (256, 38, 38) |
| 54 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 55 | shortcut | [54, 52] | (512, 38, 38) |
| 56 | convolutional | (512, 38, 38) | (256, 38, 38) |
| 57 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 58 | shortcut | [57, 55] | (512, 38, 38) |
| 59 | convolutional | (512, 38, 38) | (256, 38, 38) |
| 60 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 61 | shortcut | [60, 58] | (512, 38, 38) |
| 62 | convolutional | (512, 38, 38) | (1024, 19, 19) |
| 63 | convolutional | (1024, 19, 19) | (512, 19, 19) |
| 64 | convolutional | (512, 19, 19) | (1024, 19, 19) |
| 65 | shortcut | [64, 62] | (1024, 19, 19) |
| 66 | convolutional | (1024, 19, 19) | (512, 19, 19) |
| 67 | convolutional | (512, 19, 19) | (1024, 19, 19) |
| 68 | shortcut | [67, 65] | (1024, 19, 19) |
| 69 | convolutional | (1024, 19, 19) | (512, 19, 19) |
| 70 | convolutional | (512, 19, 19) | (1024, 19, 19) |
| 71 | shortcut | [70, 68] | (1024, 19, 19) |
| 72 | convolutional | (1024, 19, 19) | (512, 19, 19) |
| 73 | convolutional | (512, 19, 19) | (1024, 19, 19) |
| 74 | shortcut | [73, 71] | (1024, 19, 19) |
| 75 | convolutional | (1024, 19, 19) | (512, 19, 19) |
| 76 | convolutional | (512, 19, 19) | (1024, 19, 19) |
| 77 | convolutional | (1024, 19, 19) | (512, 19, 19) |
| 78 | convolutional | (512, 19, 19) | (1024, 19, 19) |
| 79 | convolutional | (1024, 19, 19) | (512, 19, 19) |
| 80 | convolutional | (512, 19, 19) | (1024, 19, 19) |
| 81 | convolutional | (1024, 19, 19) | (255, 19, 19) |
| 82 | yolo | (255, 19, 19) | |
| 83 | route | [79] | (512, 19, 19) |
| 84 | convolutional | (512, 19, 19) | (256, 19, 19) |
| 85 | upsample | (256, 19, 19) | (256, 38, 38) |
| 86 | route | [85, 61] | (768, 38, 38) |
| 87 | convolutional | (768, 38, 38) | (256, 38, 38) |
| 88 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 89 | convolutional | (512, 38, 38) | (256, 38, 38) |
| 90 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 91 | convolutional | (512, 38, 38) | (256, 38, 38) |
| 92 | convolutional | (256, 38, 38) | (512, 38, 38) |
| 93 | convolutional | (512, 38, 38) | (255, 38, 38) |
| 94 | yolo | (255, 38, 38) | |
| 95 | route | [91] | (256, 38, 38) |
| 96 | convolutional | (256, 38, 38) | (128, 38, 38) |
| 97 | upsample | (128, 38, 38) | (128, 76, 76) |
| 98 | route | [97, 36] | (384, 76, 76) |
| 99 | convolutional | (384, 76, 76) | (128, 76, 76) |
| 100 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 101 | convolutional | (256, 76, 76) | (128, 76, 76) |
| 102 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 103 | convolutional | (256, 76, 76) | (128, 76, 76) |
| 104 | convolutional | (128, 76, 76) | (256, 76, 76) |
| 105 | convolutional | (256, 76, 76) | (255, 76, 76) |
| 106 | yolo | (255, 76, 76) |
Though our example above used a 7×7 grid, the actual network makes predictions on 19×19, 38×38, and 76×76 grids (for a 608×608 input image). Three different anchor boxes are used at each scale for a total of nine anchor boxes. This is illustrated in the images below, where the cell grid and anchor boxes (scaled relative to image dimensions) are shown for each YOLO prediction layer, i.e., for layers 82, 94, and 106. The positions of the anchor boxes don’t mean anything; they’ve simply been arranged to show each one clearly.
First YOLO layer (19×19) anchor boxes—predict largest objects in
image:

Second YOLO layer (38×38) anchor boxes:

Third YOLO layer (76×76) anchor boxes—predict smallest objects in
image:

The key takeaway is that the later YOLO layers learn more fine-grained features while incorporating information from earlier layers via the route connections, ultimately using this information to make predictions on smaller scales.
Post-processing
Altogether, the three YOLO layers make (19*19 + 38*38 + 76*76) * 3 = 22743 predictions. By filtering out detections below some nominal probability threshold (e.g., 0.15), we eliminate most of the false positives. However, since each grid cell makes 3 predictions and multiple cells are likely to detect the same objects as their neighbors, we still end up with a lot of duplicate detections. These can be filtered out via non-maximum suppression (NMS). This process (all detections –> probability thresholding –> duplicate elimination via NMS) is shown in the animation below. The top frame and bottom frame of the animation are identical except the top excludes object labels, since they obscure some of the detected objects.

Conclusion
These are the basic principles underlying a YOLOv3 detection pipeline. Stay tuned for the next post, in which we’ll take a closer look at the actual implementation for real-time detection.
