In the last two posts, we explored the theory behind the Jacobian inverse method for solving the inverse kinematics of a system:
Inverse kinematics using the Jacobian inverse, part 1 Inverse kinematics using the Jacobian inverse, part 2
It’s assumed that you’ve either read those posts or already have a good understanding of how the Jacobian inverse method works. As the title suggests, this post has two major goals:
- To animate the Jacobian inverse method in Python and visualize its limitations.
- To learn about creating interactive plots in matplotlib.
The end result
This video demonstrates the Jacobian inverse method in action. The dashed circle represents the maximum reach of the arm, which is based on the lengths of all the individual links. We see that it works for any arbitrary number of joints, and we get an idea of how it tracks a moving target when the end effector is made to move at a constant velocity. We also see one of its major drawbacks, which is its instability at singularities—notice how, when the target is outside the reach of the arm, or when the location of the target forces the arm to straighten out, the joint angles change suddenly and erratically. There are several alternatives and improvements to the Jacobian inverse method that address these issues, but we won’t get into those in this post. Instead, we’ll see how to produce the animations from the video in Python.
The code, part 1
We will create two files, RobotArm.py and jacobianInverse.py, which you can find on Github.
First, create a file named RobotArm.py, or get it from the Github link above.
|
|
We start by defining a class, RobotArm2D. This class will contain the joint
angles of our robot arm, the Cartesian coordinates of each joint and the end
effector, and the length of each link of the arm. Note that, even though our
robot arm exists in two dimensions (the XY plane), we’ll use a 3D
representation in our code, not only because this will be more generalizable in
case we wish to extend our system to three dimensions, but also because
it’ll simplify some of the math, namely the use of cross products.
Technically, we’re working in 4D—our position vectors contain a
dummy fourth coordinate for use with 4×4 transformation matrices, which
perform both rotation and translation.
The __init__() method of our class, i.e., the constructor, has two optional
keyword arguments: xRoot and yRoot. These set the location of the root
joint, i.e., the first joint of the robot arm. If omitted, they default to 0,
which is accomplished by the get() method of the kwargs dictionary. Class
instantiation in Python via the __init__() method, as well as functions of a
class, are discussed in a little more detail in this blog’s very first
post, titled Visualizing K-means clustering in 1D with Python. We also
initialize the 1D array thetas, which will contain the joint angle of each
joint, and the 2D array joints, in which each column will be a 4D position
vector representing the coordinates of a joint. The first column in joints
will be the root joint and the last column will be the end effector. Finally,
lengths is a list that will contain the length of each link.
|
|
To actually add joints/links to our robot arm, we define the function
add_revolute_link(). Note that this allows us to add any arbitrary number of
joints. Only the length of the link corresponding to the added joint is
required. The initial angle can be specified if desired. The end of the last
link is taken to be the end effector.
|
|
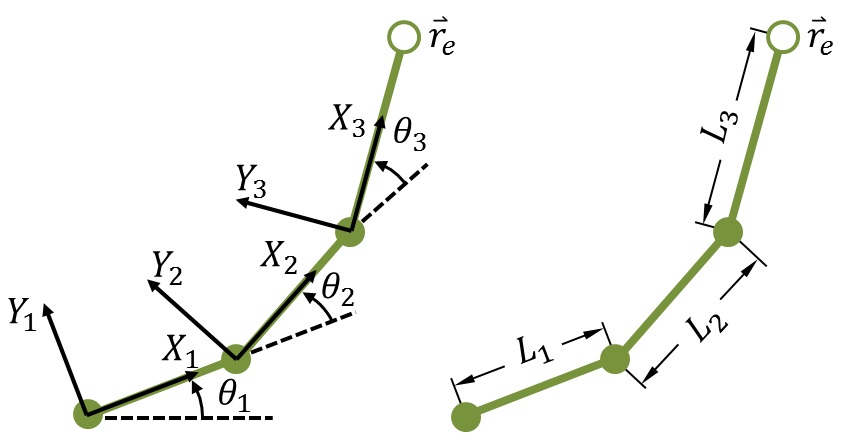
The function get_transformation_matrix() will be used to get 4×4 the
transformation matrix corresponding to each joint’s coordinate system. The
coordinate systems (and resulting transformation matrices) for the arm are
defined as in this previous post:
|
|
The function update_joint_coords() updates the coordinates in joints based
on the angles in thetas. The function works its way up from root joint to end
effector. The transformation matrix for converting coordinates from the root
joint coordinate system (“1”) to the global coordinate system
(“0”) is \([^0 T_1]\). The coordinates of the root joint, in the
first column of joints, are given by xRoot and yRoot and do not change.
The transformation matrix to convert from the second joint’s coordinate
system (“2”) to the root joint coordinate system (“1”)
is \(\left[^1 T_2\right]\). To convert from the second joint system to the global system,
these matrices are multiplied:
\(\left[ ^0 T_2 \right] = \left[ ^0 T_1 \right] \left[^1 T_2\right]\). This is
what lines 63-65 accomplish. For each \(i^{th}\) iteration, the transformation
matrix from the previous iteration (which converts from system \(i-1\) to
the global system) is multiplied with the transformation matrix from the current
iteration (which converts from system \(i\), i.e., the current joint, to system
\(i-1\), i.e., the previous joint). For the third joint, lines 63-65
would take the transformation matrix \(\left[ ^0 T_2 \right]\) and multiply it with the
transformation matrix for the third joint, \(\left[ ^2 T_3 \right]\):
\(\left[ ^0 T_3 \right] = \left[ ^0 T_2 \right] \left[ ^2 T_3 \right]\). In
this way, the coordinates of each successive joint are
converted to the global coordinate system. Since we’ve defined the end
effector to be a vector in the final coordinate system, we multiply that vector
by the final transformation matrix to get its coordinates in the global system.
As a side note, observe on line 66 that I enclosed the second index of
joints in brackets: self.joints[:,[i+1]]. The reason for this is to preserve
the shape of the original array. That bit of code extracts all rows of column
i+1 as a two-dimensional, 4×1 array. If, instead, we’d used
self.joints[:, i+1], that column would have been “flattened” into
a 1D array of 4 elements, potentially leading to incompatibilities when trying
to multiply it or add it to other arrays. This is an important thing to note
about numpy arrays: an array of shape (4,1) is 2D, and is not the same as an
array of shape (4,), which is 1D, even though both arrays contain 4 elements.
|
|
The function get_jacobian() utilizes the cross product to compute each column
of the Jacobian matrix (see the previous post for more on this), using the
unit vector pointing along the axis of rotation for each joint. In our
simplified 2D case, the axis of rotation for every joint points along the \(Z\)
axis, i.e., \(\hat{k}\).
|
|
The last part of the class is a function, update_theta(), that does exactly
what the name suggests. We use the flatten() method of the input array to
“flatten” it to a 1D array, so we can add it to the 1D thetas
array.
The code, part 2
Now, we’ll utilize the class we just created to animate the algorithm using an interactive plot. Create a file named jacobianInverse.py, or get it on Github.
|
|
First, the necessary imports, including the file we created in the last section. We create an instance of the class, add several joints, update the joint coordinates, and initialize the target location to the initial end effector location.
|
|
Next, we create the plot. The argument figsize=(5,5) to plt.subplots() on
line 19 sets the figure size; in this case, the goal is simply to set the
height and width equal so the figure is square. On line 20, we use
subplots_adjust() to position the axis limits at the edges of the figure, so
the axes take up the entirety of the plot.
|
|
Now, we compute the reach of the arm and use it to set the axis limits, with some white space at the edges, then plot a circle to indicate the boundaries of the arm’s reach.
|
|
Lines 36-41 define a function, update_plot(), to update the coordinates of
the arm and end effector plot objects. Line 43 runs this function to
initialize these plot objects with the coordinates from the arm object.
|
|
The function move_to_target() actually performs the Jacobian inverse
technique, or at least one iteration of it. Line 50 sets how far to move the
end effector on each iteration (each update of the arm’s position), as a
fraction of the arm’s reach, which essentially scales the arm’s
motion to its total length. Basically, this sets the velocity of the end
effector, if you think of each iteration as a unit of time, as long as the end
effector is farther from the target than the distance specified by line 52
(if it’s closer, then it’s considered sufficiently close, and
doesn’t move). On lines 53-54, we get the unit vector in the direction
of the target from the end effector. On line 55, we compute \(\Delta \mathbf{r}\),
or the vector distance that we’d like the end effector to move (toward the
target). The rest of the function computes the Jacobian based on this vector,
inverts the Jacobian, computes the change in joint angles, then updates the
joint coordinates and the plot with the new arm configuration.
|
|
Now, we arrive at the interactive stuff. First, we define the variable mode,
which will assume a value of 1 or -1. Mode 1 signifies that the target will be
set manually whenever the user left-clicks somewhere within the plot. Mode -1
signifies that the target will move on its own along a predefined path. This
first function, on_button_press(), is responsible for setting the target
manually when mode is set to 1.
In matplotlib, event callbacks are defined by a function that takes an event
object as an input (whenever an event, like a button click or a key press,
occurs, this event object is sent automatically to the function). The event
object contains information about the event. In the case of a mouse click, this
includes the x and y coordinates, with respect to the plot axes, of the click,
which we obtain on lines 72-73. In the conditions on lines 77-78, we
check that we’re in the correct mode, that the button equals
“1” (“1” denotes the left mouse button), and that the
click was within the axis limits (if it wasn’t, the type of the returned
coordinates would be None instead of float). Line 81 associates the button
press event with the figure via the function on_button_press().
|
|
Next, we do the same thing for a key press event. We’d like the script to
terminate if the Enter key is pressed, by setting exitFlag to True. Moreover,
we’d like to toggle the mode if the Shift key is pressed. As above, we
check whether either of these buttons is pressed and act accordingly. On line
95, we connect the key press event to the figure.
|
|
Finally, after turning on interactive plotting and showing the plot, we employ a
while loop to continuously run our move_to_target() function. This way, the
arm will track the target any time it moves. If mode is set to -1, the target
moves in a pseudo-random fashion, which we accomplish using the continuously
changing variable t and, on lines 107-108, a few strategically placed sine
and cosine terms. I say “pseudo-random” because, of course, the
sines and cosines mean it’s actually cyclical.
The last line, line 113, is required to update the plot after button or key
press events. I utilize the figure canvas’s get_tk_widget() method
because I’m using the Tkinter backend, so this may be different if
you’re using a different backend. Tkinter is the default Python GUI
package, and allows us to create GUIs and graphical objects, like plots.
Matplotlib is able to work with a variety of different GUI backends, like GTK,
Qt, and Wx, to name a few. You can check the GUI backend currently being used
with the command plt.get_backend(). You can also list all backends available
on your system by importing matplotlib with import matplotlib followed by the
command matplotlib.rcsetup.all_backends.
Conclusion
That was a long post, but you now have a functioning script that’ll
interactively animate the Jacobian inverse technique. Try playing around with
the parameters of the inverse kinematics algorithm to see how it affects the
ability of the arm to track a target. For example, set the threshold for the
distance between the end effector and target on line 52 of
jacobianInverse.py to a value smaller than distPerUpdate and see what happens;
since you’d be setting the threshold to a value smaller than the distance
the end effector moves during each iteration of the algorithm, the end effector
might infinitely overshoot the target without being able to reach it. You can
also adjust the value by which t is incremented on line 111 to change the
speed of the target in the moving target mode.
Try adding more joints/links to the arm. An easy way to add a lot of joints in one go is with the following code:
for i in range(20):
Arm.add_revolute_link(length=3)As for interactive plotting, we’ve just barely scratched the surface. Read
the matplotlib documentation on event handling for more on the different
types of events. One idea might be to make a plot in which the arm tracks your
mouse cursor using the motion_notify_event.
